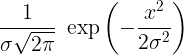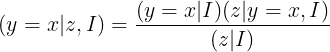Reading Jaynes: Fear not the unknown unknown
From time to time, I’ll post and comment on excerpts from the works of E. T. Jaynes and other scientists which are particularly interesting or insightful. Here’s one that might change how you think about dealing with uncertainty.
“… because as we know, there are known knowns; there are things we know we know. We also know there are known unknowns; that is to say we know there are some things we do not know. But there are also unknown unknowns—the ones we don't know we don't know.”
— US Secretary of Defense Donald Rumsfeld, 2002
I find that people often hesitate to apply probability to a real situation, because there are too many uncertainties. That’s a real problem, because conditions of great uncertainty is exactly when we should apply probability. But in math class we only learn to apply probability in textbook situations, like rolling dice or shuffling cards. At best, there will be some word problem where a new medical test has a 10% false positive rate and a 20% false negative rate, so how should a particular result inform your diagnosis?
In real life we don’t get the numbers handed out like a textbook problem, ready to plug into the equations on our formula-sheets. So it’s tempting to put up our hands and say “I just don’t know the probabilities”, as though probability meant anything other than a lack of certainty to begin with.
You can always apply probability, not matter how uncertain you are. And the less certain you are, the more reason there is to use it.
Let’s take a look at an example.
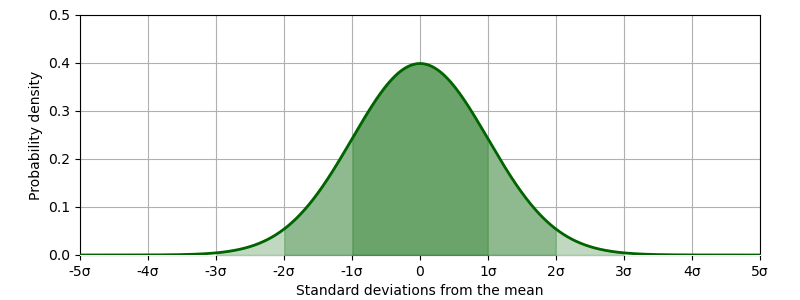
The Gaussian distribution (also known as the normal distribution or the bell curve) is one of the probability distributions that almost everybody learns about at some point (even if most have forgotten it by now), and almost the only probability distribution used daily by anyone who isn’t specialized in statistics. It’s the one that tends to be referenced by any mention of “standard deviation”, whether in terms of measurement noise, stock market moves, clothing sizes, medicine effectiveness, and so on, or when they say “a six-sigma event”.
In fact, it’s often the first distribution anyone reaches for even in situations where there’s no good reason to believe the process are really Gaussian-distributed at all. And why would it be Gaussian anyway? After all there are a whole host of other shapes of common probability distributions that come up in all sorts of situations. Some are bell-curve-like, resembling the Gaussian but with longer tails, some are lopsided and funny-looking, some are flat and boring, some are more jagged, and so on.
And yet most of the time, when you open a textbook in any field other than statistics itself, flip to any page with a random variable in the equation and the first paragraph will start with a sentence like “… we assume the errors are independent and gaussian-distributed…”.
Mathematicians and students alike frequently wonder why this particular curve comes up so often (while others are content to just use it and move on). The usual answer is the central limit theorem: this curve tends to result any time a large number of independent random results are added together, like the sum of a handful of rolled dice or a load of balls bouncing through a grid of pins.
When the central limit theorem is at work, as it often is in nature, it’s indeed very reasonable to expect a Gaussian to result. But Gaussians seem to work unreasonably well in calculations even when no such process is at work. A cynic might say they just get used out of convenience — they’re mathematically simple, which results in nice-looking calculations, they have a host of nicely-behaved properties, and they’re familiar. But Jaynes has a very different take, which he presents with his usual charisma.
Excerpts below are from E. T. Jaynes, in chapter 7 of Probability Theory: The Logic of Science.
In the middle 1950s, [Jaynes] heard an after-dinner speech by Professor Willy Feller, in which he roundly denounced the practice of using Gaussian probability distributions for errors, on the grounds that the frequency distributions of real errors are almost never Gaussian.1 Yet in spite of Feller’s disapproval, we continued to use them, and their ubiquitous success in parameter estimation continued[…] the same surprise was expressed by George Barnard (1983): “Why have we for so long managed with normality assumptions?”
Today, we believe we can, at last, explain (1) the inevitability ubiquitous use, and (2) the ubiquitous success, of the Gaussian error law. Once seen, the explanation is indeed trivially obvious; yet, to the best of our knowledge, it is not recognized in any of the previous literature of the field, becuase of the universal tendency to think of probability distributions in terms of frequencies. We cannot understand what is happening until we learn to think of probability distributions in terms of their demonstrable information content instead of their imagined (and, as we shall see, irrelevant) frequency connections.
Jaynes then presents four famous historical derivations of the Gaussian equation, each arriving at the same result from different directions and assumptions, before essentially dismissing all of them:
We started this chapter by noting the surprise of de Morgan and Barnard at the great and ubiquitous success that is achieved in inference — particularly, in parameter estimation — through the use of Gaussian sampling distributions, and the reluctance of Feller to believe that such success was possible. It is surprising that to understand this mystery requires almost no mathematics — only a conceptual reorientation toward the idea of probability theory as logic.
Let us think in terms of the information that is conveyed by our equations. Whether or not the long-run frequency distribution of errors is in fact Gaussian is almost never known empirically; what the scientist knows about them (from past experience or from theory) is almost always simply their general magnitude.
(For example, your digital multimeter has an accuracy rating printed in the manual that says “1% rms error”, and that might be about as much as you know about your measurement errors when you take measurements with that multimeter).
[A physicist] seldom knows any other property of the noise [beyond the mean-squared-error]. If he assigns the first two moments of a noise probability distribution to agree with such information, but has no further information and therefore imposes no further constraints, then a Gaussian distribution fit to those moments will, according to the principle of maximum entropy as discussed in Chapter 11, represent most honestly his state of knowledge about the noise.
The “first two moments” of a probability distribution are the mean, and the variance — the square of the standard deviation. What Jaynes is saying is that if all you know is the mean and the standard deviation of your measurement, then with that information, you simply cannot do better than a Gaussian distribution. To use any other equation, any other curve, would be introducing the assumption of additional knowledge beyond just the mean (the number you read on your multimeter screen) and deviation (the accuracy rating printed in the manual).
Jaynes explains that the reason that a Gaussian is the best is because it’s the curve that maximizes entropy. In other words, any other curve would either represent additional information, or else would not have the same mean and variance as our multimeter reading.
If you do have that additional knowledge, you can use it, and you’ll get a better result. For example, if you’re measuring the resistance of a resistor you found in your electronics drawer and you measure it as 0.2 ± 0.5 Ω, then well… it’s very unlikely to have negative resistance, so you shouldn’t hesitate to clip off the tail of the distribution that falls below 0 Ω. (And then learn to use a more appropriate measurement technique).
But if you don’t have that kind of supplemental information, then a Gaussian distribution may be the best you can do based on what you know. So, don’t be afraid to go ahead and use it!
For some people, this comes as a big change in how to think about uncertainty. You don’t need to know that an error is Gaussian to justify treating it a Gaussian and proceed with your calculations. You simply need no reason not to.
For this reason, whether our inferences are successful or not, unless such extra information is at hand, there is no justification for adopting a different error law; and, indeed, no principle to tell us which different one to adopt. This explains the ubiquitous use. Since the time of Gauss and Laplace, the great majority of all inference procedures with continuous probability distributions have been conducted — necessarily and properly — with Gaussian sampling distributions. Those who disapproved of this, whatever the grounds for their objection, have been unable to offer any alternative that was not subject to a worse objection[…]
It is now clear that the most ubiquitous reason for using the Gaussian sampling distribution is not that the error frequencies are known to be — or assumed to be — Gaussian, but rather because those frequencies are unknown. One sees what a totally different outlook this is than that of Feller and Barnard; ‘normality’ was not an assumption of physical fact at all. It was a valid description of our state of knowledge. In most cases, had we done anything different, we would be making an unjustified, gratuitous assumption (violating one of our Chapter 1 desiderata of rationality).
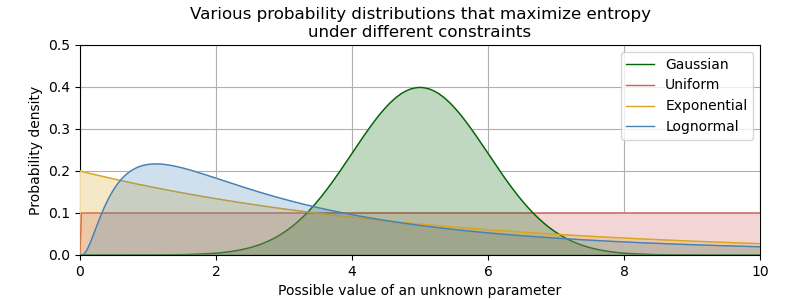
In fact, this principle does not apply only to the Gaussian distribution.
When all we knew about a measurement was its mean and its variance, then the best representation of our knowledge was a Gaussian bell curve. And that might be the most typical scenario. But we do sometimes find ourselves in other situations, knowing other things.
In this case, we have to return to the same principle of maximum entropy that came up earlier, and see how we can use it in other situations.
I don’t want to dive too deep into math and measure theory here, but entropy is basically a measure of how much or how little information is communicated by some data (or by a probability distribution). In essence, the broader a probability distribution is, the higher its entropy. A very narrow pin-point curve represents very low entropy (and a lot of certainty about some value). A broad, even distribution represents high entropy and high uncertainty about some value.
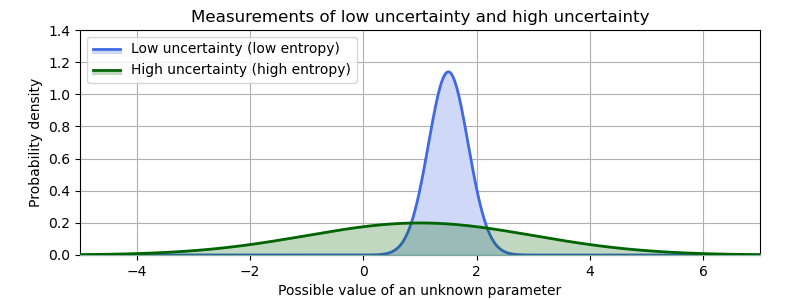
The principle of maximum entropy says: “if you don’t actually know something, don’t fake it. Make the distribution as broad as it takes to only represent what you actually do know”.
If you really want to show off, you can derive the maximum entropy distribution for your specific situation using Lagrange multipliers and variational calculus (the art of deriving functions that maximize a value subject to constraints). But for the rest of us, there is Wikipedia’s ready-made list of maximum-entropy distributions.
This will get you a long way! Gaussian distributions already get you far enough as it is. Being able to go beyond is almost a superpower, which lets you start to reason about long-tailed distributions, unknown-unknowns, and black swans. There’s a good chance that any other distribution you’re likely to need (or at least use as a starting point) will be somewhere on that list, and all you have to do is understand how to find it.
To get your distribution, there will be two things you need: support, and maximum entropy constraint. You should be able to get both of them by thinking about the nature of the sort of value you’re trying to reason about.
(Magnitude of the next earthquake? The prediction of annual maximum rainfall? Size of an insurance claim? Number of orders in an upcoming quarter? Interval between train arrival times?)
In any sort of parameter estimation situation, you will be primarily concerned with three things:
y: the (unknown) quantity you’re trying to estimate or predict;
x: one, of several, plausible values for y;
(y = x | I): the probability that the true value of y is equal to x, given what information we know, and the function we’re trying to find somewhere on this table.
Support means the set of plausible values for x. A moment’s thought lets us narrow down the table substantially based on support:
There’s no such thing as half a customer, so the number of orders next quarter will be an integer (if we treat product returns as negative) or a natural number (if we don’t): ℤ = {…-3, -2, -1, 0, 1, 2, 3…} or ℕ = {0, 1, 2, 3…}
The resistor we pulled out of the drawer has no upper limit to its resistance (it could be an open circuit) but is probably neither a superconductor nor a perpetual motion machine, so its resistance will higher than 0: (0, ∞)
The interval between train arrival times likewise can’t be less than zero, but it’s plausible that two trains could arrive at the exact same time. On the other hand, it’s also plausible that the next train will never arrive, so: [0, ∞]
The angle that a spinning roulette wheel settles will be somewhere on the circle, so: [0°, 360°) or in radians: [0, 2π)
The outcome of an upcoming coin flip or presidential election: {heads, tails}
Maximum entropy constraint describes the rest of what we know. Ask yourself: do you have any information regarding:
What the expected outcome might be? — E(x)
How far it might be from its average? — E((x - μ)²)
How far it might be from zero? — E(x²)
What its expected magnitude might be? — E(ln(x))
What ratio it might be of its average? — E((ln(x) - μ)²)
(And so on.)
This is a surprisingly powerful technique. Even without a strong background in statistics or variational calculus, you can quite quickly hone in on one candidate function for the situation you’re trying to understand, model, or predict. This isn’t cheating; we won’t get anything from this function that we didn’t already know. But it will help us mathematically represent what we already knew, in a form that we can do computer calculations with.
More importantly, this technique helps us quantify what we don’t know. By sticking to maximum-entropy distributions, we reduce the chance that we’ll bias our estimates with any assumed information that we didn’t actually have. The price is a less narrow, less confident, less decisive-looking distribution, but that’s just the price of honesty, and it’s always worth paying.
If you’re familiar with using Bayes’ rule, this procedure is especially useful for getting prior probability distributions (y=x|I), which is often the frustrating point where people get stuck right at the very start of a probability calculation. Once you have your prior, it’s a comparatively easy and mechanical process to update it with whatever measured data you have (z).
If your data is conclusive, the posterior will pin-point the right answer pretty quickly even if your prior was very broad to start with. So the real value of using this process to get an honest prior is when your data is inconclusive.
Either way, the important thing is to be honest about what you do and do not know — both with yourself, and with your model. Maximum entropy methods enable that in a powerful way. And guided by that principle, you don’t need to know what distribution your data is actually drawn from in order to proceed with a completely valid probabilistic analysis. You only need to be comfortable acknowledging the unknown.
This post isn’t intended as professional engineering advice. If you are looking for professional engineering advice, please contact me with your requirements.
Jaynes uses the term “frequency” here in the sense of frequentist probability: how often a particular value comes up, like how often a rolling a die results in a 6. Given that These Are Systems also covers control theory, I should point out that this is not to be confused with temporal frequency. A probability theorist hears the phrase “coin flip frequency” and thinks about how often a single coin flip tends to land ‘heads’ relative to ‘tails’, while a physicist is thinking about how fast the coin is rotating in mid-air, and a control theorist is thinking of how many times they can flip the coin per second using their servo-controlled coin-flipping robot.