In a recent series I’ve been discussing the lighthouse problem: trying to identify the coordinates of a lighthouse at sea based on only sporadic recordings of its light hitting the shoreline. First, I walked through the powerful, but computationally expensive, purely Bayesian approach. Then I introduced the Kalman filter as an efficient alternative, and we saw how, even though it should be theoretically incapable of tackling that problem, it turned out to be easy to make it work very well with just a few small tweaks.
Even so, I’ve only demonstrated half of the Kalman filter’s power: the update step, which processes new data. The Kalman filter also includes, as part of its machinery, a prediction step, which takes the probability distribution as of timestep k and extrapolates a new distribution for timestep k+1. Because a lighthouse by its nature doesn’t move, that prediction step changed absolutely nothing, so I got away with neglecting it until now.
Today we’re going to replace the lighthouse with a moving ship. We’ll need to add prediction into our Kalman filter to keep up, and we’ll see how this, too, follows from the Bayesian probability rules.
By the way… I’m not actually obsessed with tracking down maritime objects! My motivation for this series is to familiarize you with how the Kalman filter approximates Bayesian reasoning, and the lighthouse problem is a testbed that is challenging-enough to keep it fun. But the problem is also more practical than it might seem. For example, it’s isomorphic to the challenge of locating the position of a radioactive tracer inside a body by using a detector array on the surface.1
So let’s reformulate the lighthouse problem to make a “ship” problem:
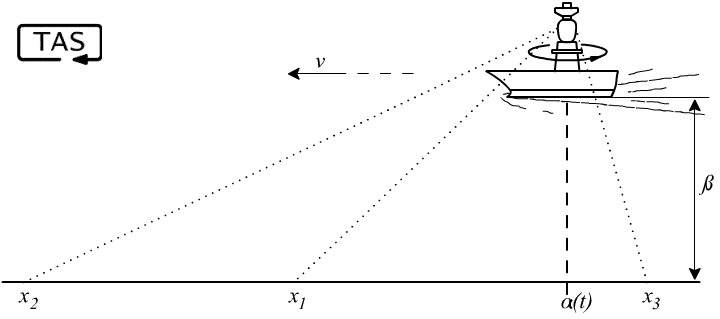
A ship is somewhere off a piece of straight coastline at position α(t) along the shore and a distance β out at sea. It is moving parallel to the shore at a constant, but unknown, velocity v m/s. It emits short highly collimated flashes at 1-second intervals but at random azimuths. These pulses are intercepted on the coast by photo-detectors that only record the time that a flash has occurred, but not the angle from which it came. Flashes so far have been recorded at positions {x₁…xₖ}. Where is the ship currently?
We could certainly make this problem even more complicated — the ship could move along a random vector; it could also accelerate; its acceleration could vary with time; we could have partial control of its acceleration; it could steer; bounce off obstacles; rise into the air; teleport unpredictably, and so on. But this already should be enough to introduce the idea of prediction, and then we can consider further mixups next time.
Here are the equations of motion for this ship:
α(t) = α₀ + vt — Moving at speed v along the shoreline
dv/dt = 0 — Speed doesn’t change
dβ/dt = 0 — Distance from shore doesn’t change
Bayes
Let’s quickly go through the Bayesian approach, so that we can compare how well the Kalman filter measures up to it. The computational difficulty is heating up as the new unknown parameter, v, introduces yet an additional dimension to consider. But as usual, we just need to start with a prior, then figure out what the parameters [α(tₖ), β, v] say about the likelihood of observing data xₖ, and then rely on Bayes’ rule to do the hard work of flipping that around to get what the data implies about α(tₖ), β, v.
Let’s start with Bayes’ theorem as always. Here is how it guides us to update on the latest measurement xₖ₊₁ to learn about the latest state y = [α(tₖ₊₁), β, v]:
And again, for those who don’t love to read math, here’s the English phrasing:
Or in even fewer words: posterior = prior × likelihood.
So to get our posterior describing the ship’s location, we need a prior and a likelihood. Let’s do it.
The once and future prior
Let’s keep the non-informative priors we used earlier: uniform for α₀, and log(β). Now we need a prior probability for v. I don’t think that the information in the problem gives us one unique choice, but remember, the most important thing about an uninformative prior is just to be sure we’re not prematurely ruling out possible true values. A quick search suggests the world maritime speed record was set in 1978 by Ken Warby’s Spirit of Australia at about 276 knots, or 511 km/hr, powered by a J34 fighter jet engine. At risk of understatement, our ship in question is unlikely to be going faster than that.
So for argument’s sake let’s make our prior for v Gaussian with a mean of 0 and a standard deviation of, say, ~250 km/hr (70 m/s). Combined with our priors for α₀ and β, we have:
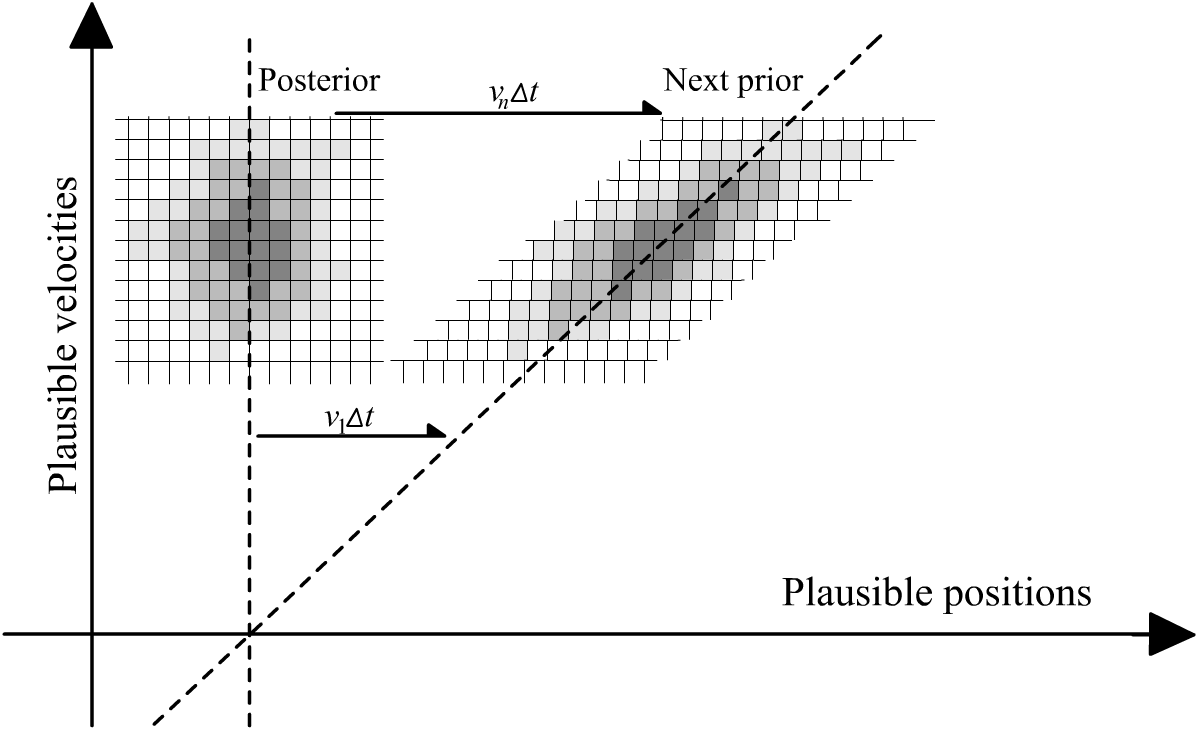
This is a good initial prior to start out with for updating on our very first data point x₁. But now here’s the important part: we need a prior for every update that we do, on every new data point, not just t₀. What about for t₁? For t₂? For tₖ₊₁?
Back when we were tracking a lighthouse, the only thing that was changing with time was our knowledge of the parameters, not their actual values. If a minute passed by with no new data, we would have no reason to change our beliefs about the lighthouse’s coordinates. So we were able to just recycle our posterior after updating on x₁ to serve as our prior when updating on x₂. This gave us a very nice recurrence relationship.
With a moving ship, our posterior for α(t₁) no longer can double as a prior for α(t₂), because we know the ship’s position will have moved over that time interval. Even if our sensors lost power for a while and we had to extrapolate the ship’s position with no new data, we could do better than just guessing it stays still.
Fortunately, the system’s equations of motion show us how to make a much better guess: α(t₂) = α(t₁) + vΔt. Plugging this into our prior allows us to look forward and adjust our probability distribution in accordance with the way the system moves:
To put this equation into words: whatever probability distribution we’d found as our posterior for α(t₁), we just shuffle it over sideways by vΔt to get the prior for α(t₂). (We don’t know v for certain, so we’ll make up for that by brute force computation: iterating this process over all plausible velocities.2)
The likelihood
The direction of the light flash isn’t directly influenced by the ship’s speed, so supposing the ship’s next position [α(tₖ₊₁), β] is already enough to get the corresponding probability distribution of the next data point xₖ₊₁. Conditional on the next-timestep state, the likelihood is still just our old Cauchy equation.
And finally… lots of turning the crank
We’ve seen how Bayes’ rule splits up into two terms, representing the repetitive application of two procedures:
Generate a new prior probability by extrapolating forward from our old posterior, and
Generate a new posterior by updating on the new data xₖ₊₁
Now getting the full Bayesian solution is just a matter of running that computation many, many, many times over a humongous grid of plausible positions and velocities.
I won’t easily be able to plot the entire 3D joint distribution, so I’ll collapse it down to just the distribution for the ship’s coordinates [α(tₖ), β], and display v by only its marginal distribution.
I’ve added a colour gradient to the measurement histogram so that the recency of each measurement is visible. I don’t know about you, but I find it impressive that the algorithm can extract such a confident, accurate picture of the ship’s motion from such scattered data!
Kalman’s turn
It took about two hours for my Thinkpad to compute the above Bayesian solution. The Kalman filter reduces that to milliseconds.
The Kalman filter advances in two steps: prediction, then update. Last time, we saw how the Kalman filter’s update process comes directly from approximating Bayesian probabilities with a Gaussian. By now it should be no surprise that the prediction step does, too.
In order to get the prior probability for Bayes’ equation, we had to use the system dynamics to shift our old posterior distribution into a new prior for the next timestep. Since we weren’t sure what those dynamics are exactly, we just iterated the process over every possibility and turned the crank. The Kalman filter’s prediction step does this job while replacing brute force with finesse.
With the Kalman filter we’re representing our beliefs by a Gaussian, so we just need to keep track of a mean and an uncertainty. Working out what happens with the mean is pretty straightforward: our best guess for α(t+Δt) would be to just take our guess for α(t) and shift it by vΔt, using our best guess for v.
So what I want to write is: μₐ,ₖ₊₁ = μₐ,ₖ + μᵥ,ₖΔt. And that would be correct, except that I was already using the symbol μₐ,ₖ₊₁ for “the mean of α after the update on the k+1th data point”. We need a different symbol to represent the intermediate state that comes after the prediction, but before the update on new data. I’ll use ͞μₐ,ₖ₊₁ to refer to “the mean value of α that is predicted for tₖ₊₁”. So, the state prediction for α is ͞μₐ,ₖ₊₁ = μₐ,ₖ + μᵥ,ₖΔt.
We also need to apply this process to the covariance — the uncertainty. If you think about it, any uncertainty we have about v should cause a gradually-increasing uncertainty about the position α. Even if we knew α(t₁) with pinpoint accuracy, by time t₂ our estimate would smear to a cloud if we didn’t know the speed of travel. As with all Gaussians, that cloud will be an ellipsoid shape. But it will be tilted in the α-v plane, because the errors should correlate: if the real v is higher than our best guess μᵥ, then the real α(tₖ₊₁) will be higher than our best guess μₐ,ₖ₊₁ and vice-versa.
Enter the matrix
The Kalman filter has us write our system dynamics in terms of a state transition matrix, F, which expresses how the present state relates to the future state. This is part of what’s called a state-space model.3 4
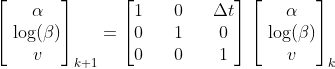
(If you’re wondering why we have log(β) as a state variable instead of β, it’s based on the finding in my previous article).
When we transform our probability distribution with F, the new (predicted) mean evolves directly from the previous mean, via that state transition matrix:5 ͞μₖ₊₁ = Fμₖ. Meanwhile the covariance undergoes the same transition, but it applies twice, basically because variance is a squared quantity.6 7 The equation for the covariance of the prediction is ͞Sₖ₊₁ = FSₖFᵀ.
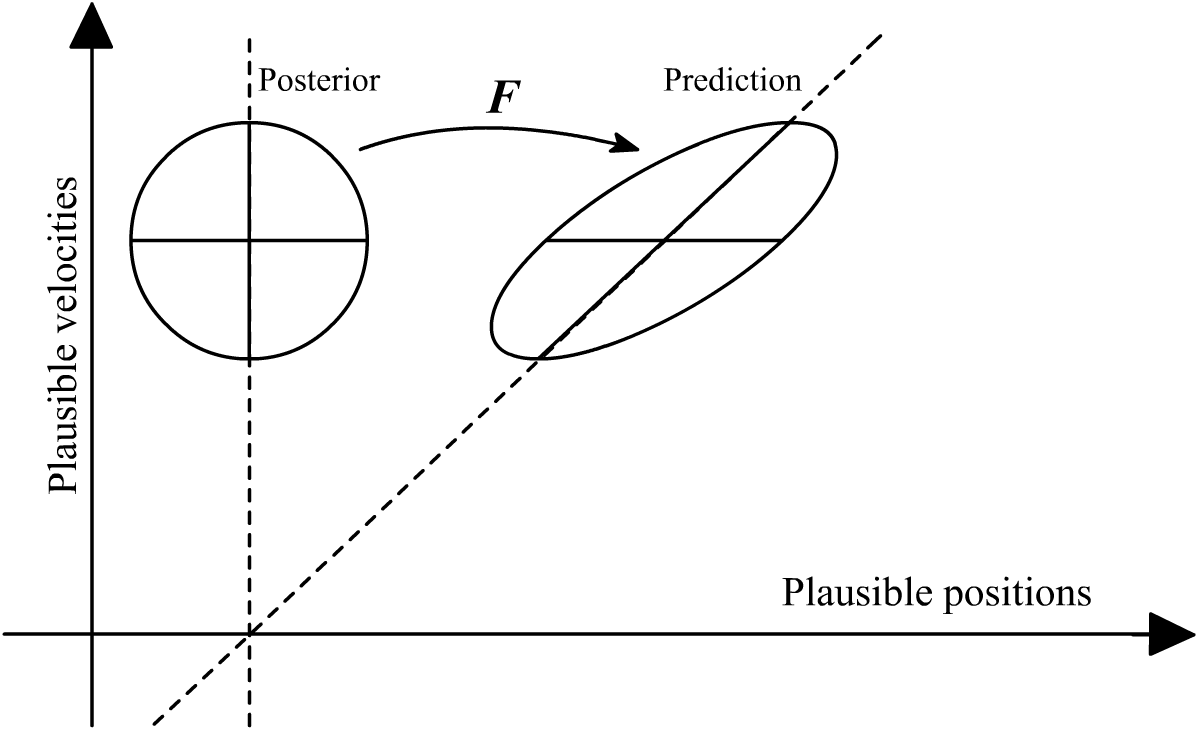
In other words, the Kalman filter’s prediction is nothing magical or surprising; we just evolve our beliefs about the system state by following the very same dynamics that we believe govern the system itself. Because how would you make any better guess than that?
Then, after making the prediction, we update on the measurement just like we did in the previous article. With each timestep, the prediction grows the covariance slightly (as we’re always a bit more uncertain about the future than the present), and then the measurement shrinks it again.
Here’s the Kalman filter at work. The prediction step is shown in red, and the update step is in pink.
As it did last time, the Kalman filter tracks extremely closely to the ideal of direct Bayesian estimation. It’s tempting to think it’s just curve-fitting the Bayes output, but you have to remember it doesn’t actually have access to that data; both solutions are being computed independently. This might be especially surprising when you remember that we’re still voiding the warranty, with noise that is about as non-Gaussian as it gets.8
Source code is available on gitlab if you’d like to follow along.
Anyway, that’s basically the prediction step of the Kalman filter in a nutshell. There are still a few more features up its sleeve to handle more complicated systems with control inputs and process noise, but they don’t change the idea very much.
If the system is strongly nonlinear, then one matrix multiplication alone won’t be enough to pull a new prior from our old posterior, and the Kalman filter won’t give good results. But we can usually fix such limitations without changing the Bayesian spirit at the heart of the technique. Any transformation — linear or otherwise — that can forecast our knowledge from t₁ to represent our most honest prior for the system state at t₂ is fair game. Techniques like the Extended Kalman Filter and Unscented Kalman Filter extend the core ideas of the Kalman filter for the case of nonlinear systems.
Final thoughts
I know these short articles aren’t enough to offer a detailed mathematical understanding of how to implement a Kalman filter well for an arbitrary system, and they aren’t intended as tutorials. Fortunately, there are many other authors who have done much more complete, and much more respectable, jobs of that.9
I hope only to have planted some seeds for the appreciation of the Kalman filter’s usefulness, its power, its flexibility, and its deep connection to Bayesian probability, with as little math as I could get away with (though still quite a bit, sorry). I hope that this helps connect the dots for those who have struggled with more in-depth tutorials, or perhaps inspired you to “void the warranty” yourself, and experiment with pushing beyond a technique’s conventional limitations.10
And even if you never have any need to filter a noisy signal or estimate a parameter, even if you never have cause to use a Kalman filter for anything, I think that it’s still a concept worth knowing about. When an idea is so simple and so powerful, it tends to show up everywhere — especially in nature. (Is the hippocampus a Kalman filter?)
The Kalman filter, of course, only captures a small part of the depth of Bayesian reasoning. But in contrast to pure Bayesian logic, which tends to spiral off into infinite loops, halting problems, and other calculations that outlast the lifespan of the sun, the Kalman filter captures reality with incredible efficiency. That, in my opinion, has earned it the right to be respected as a basic building block of system theory, prediction, and even perception in general.
This post isn’t intended as professional engineering advice. If you are looking for professional engineering advice, please contact me with your requirements.
Applications of this technique that I’ve seen in the literature tend to use detectors on all sides. However by using the Cauchy distribution in the style of the lighthouse problem, a single flat detector plane should be sufficient to localize a radioactive particle in 3D space; depending on the source intensity, this could be accomplished pretty cheaply with a camera and a plastic scintillator sheet.
This requires discretizing the possible velocities into a grid, just as we did with position. As with any discretization process, there is a tradeoff to be made in terms of resolution vs. memory & computation time. There are ways to save some time and memory, such as refining the grid density to be denser in areas of high probability and sparser in areas of low probability.
State-space form is, basically, taking a system described by differential equations and, at least if that system is linear, organizing those equations in the following traditional format:
where x is called the state vector and contains all the data about the internal state of the system; u is the input vector, containing whatever inputs might be applied to the system; y is the output vector, containing whatever important properties we care about extracting from the system. (Note that in my articles I have been using ‘x’ to denote sensor measurements, not state, following the phrasing of the lighthouse problem). A, B, C, and D are matrices that describe all the connections between the state variables, their rates of change, and the inputs and outputs. If A, B, C, and D do not vary with time, the system is called time-invariant.
This ship system has no inputs, so B and D are empty. If we’re interested in displaying the ship’s full state [α(t), β, v], then y = x, so C is a 3x3 identity matrix. And last but not least, the system matrix A contains our system’s equations of motion:
Representing differential equations in state-space form is popular, compact, and versatile format. It serves as a common “user interface” to a lot of techniques and computer algorithms, including the Kalman filter. So the first step in many controls and modelling problems is to get a state-space representation of the system.
That said, there are some systems that are difficult to express this way. Nonlinear systems require relaxing the formatting constraints a little bit. Fractional-order systems, even when linear and time-invariant, sort of break the entire idea behind this approach, and are easier to just express as a list of transfer functions.
The state transition matrix F is essentially a discrete-time version of A. Rather than represent the relationship between x(t) and its rate-of-change, it represents the relationship between x(tₖ) and its subsequent value x(tₖ₊₁). For time-invariant systems it can be calculated from A by the matrix exponential: F = expm(A Δt).
If we had data about any control inputs to our system uₖ, we could incorporate that data into our prediction by expanding the equation a little bit: μₖ₊₁ = Fμₖ + Guₖ. The effect of the inputs uₖ on the state variables are quantified by G, the input transition matrix. G serves the same role in the discrete-time model that B serves in the continuous-time model, just like F relates to A.
To elaborate, if X is a random variable (such as our state vector) over which we have some probability distribution, and F is a linear transformation applied to X, and E(X) denotes the “expectation of X” (which is another way of saying the mean of X, which we can also write μ), then:
E(FX) = FE(X) = Fμ
cov(FX) = E( (FX - Fμ) (FX - Fμ)ᵀ) = F E( (X - μ) (X - μ)ᵀ) Fᵀ = F cov(X) Fᵀ
But I think “the transformation applies twice, because variance is a squared quantity” is a bit more intuitive and much easier to remember.
By the way, we can also add in an fudge factor for additional uncertainty, called process noise, representing both unmeasured external disturbances as well as any further doubts we might have in the model itself. This just adds a little extra to the covariance with each prediction step. For example, we could use this if we thought the ship velocity might be actually varying a bit with time. Then even if we’ve pinpointed the velocity at time t₁ with our measurements, we will lose some confidence in our forecast of that velocity for time t₂, as we ought to.
When a model is built on strong mathematical foundations, it might not make much sense to include additional process noise. For example, adding a process noise term to the covariance of α would suggest that (somehow?!) we aren’t confident that the velocity is the only thing that could contribute to α changing over time. Since the change in α over time is the velocity by definition, that seems like a mistake. If we wanted to represent a little extra uncertainty in the ship’s position for whatever reason, the measurement noise term might be a more sensible place to put it.
In fact it’s so far from Gaussian that even the central limit theorem itself doesn’t save us; while most random variables will eventually converge to Gaussian when you average them all together, averaging together any number of Cauchy-distributed variables still just leaves you with a Cauchy distribution no matter how much data you collect.
It’s actually surprising how much literature exists about the Kalman filter specifically, especially tutorials and derivations, and a lot of it is exceptionally well-presented and approachable. I really hesitated to write a series about it for that reason, because I didn’t want to add noise to an already clear signal. But I plan to refer to the Kalman filter a fair bit in future articles, and it seemed negligent to not at least provide a basic and intuitive, if slightly incomplete, foundation.
This is why I haven’t gone deep into the weeds on control inputs, process noise, how to appropriately derive the measurement covariance matrix, and so on. What I really want to cover here is not rote tutorials or dusty proofs, but rather less-trodden ground. Interesting questions that lurk in the night, ready to strike curious-minded engineers, whose answers are frustratingly hard to find on the internet or in literature.
(Rather like attaching a fighter jet engine to a boat in order to claim the world speed record.)




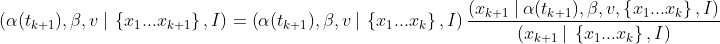
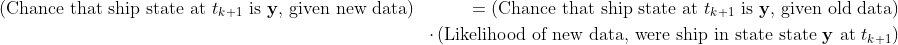

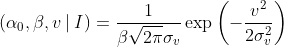
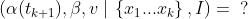
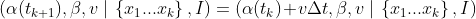
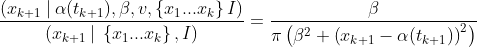


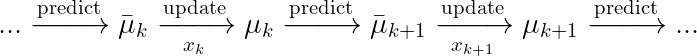
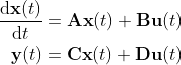

I'm wondering if in some situations, a Kalman filter simplifies to equations that are easy to implement? What do degenerate forms of it look like?