When a technology becomes digital, its rate of growth no longer obeys a linear equation. It will look more like this:
[gif of a bacteria population doubling slower than a linear system would]
— “If you want exponential growth, forget linear thinking”, Matter.vc
With all the business workshops disparaging “linear thinking” in a world of exponential growth, it might be surprising to hear that linear systems are what produce exponential growth. In fact, I’d argue that the widespread abundance of exponential growth is a reflection of just how commonplace linear systems are.1 2
It’s one thing if your revenues are growing exponentially, but for engineers, exponential growth — in say, the reactor pressure — is usually a very bad sign.
We call a system unstable if, when left to its own devices, it tends to run away with ever-accelerating growth. Both linear and nonlinear systems can be unstable. Unstable linear systems grow exponentially, which makes them challenging enough to deal with; nonlinearity can make that even worse, because nonlinear systems can grow super-exponentially.3
Keeping unstable systems under control is an inherently difficult task, for which good controller design is only the start. Every single component of the system needs to be capable of responding faster than the unstable growth rate, or else stabilization is impossible.
In my article about right-half-plane zeros, I mentioned that between zeros and poles, the poles get all the attention. Well today, we’re indeed talking about poles after all.
Remember, systems are governed by differential equations, and zeros and poles are a description of those equations — intrinsic properties of the system itself. The zeros describe how a system responds in the short term to an input, whereas the poles describe how it reacts in the long term: does it settle back down after that initial nudge, or does it grow and grow?
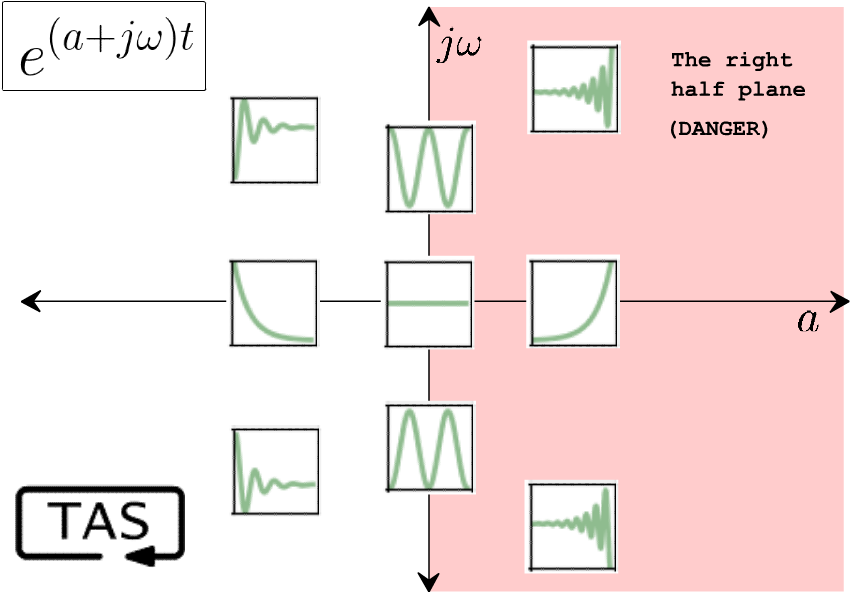
The measure of an unstable pole is its growth rate, which is its distance from the origin along the a axis (the “real” axis). Faster-growing exponentials are more unstable than slow-growing ones, and correspondingly more troublesome to deal with.
Whether the system is linear or nonlinear, an instability is usually a sign of positive feedback occurring somewhere inside that system, where the output of some process causes growth in its inputs (which causes more growth in its outputs, which- [BANG!!]). In a nuclear chain reaction, a neutron strikes an atom and causes it to split, releasing more neutrons which strike more atoms: positive feedback.4
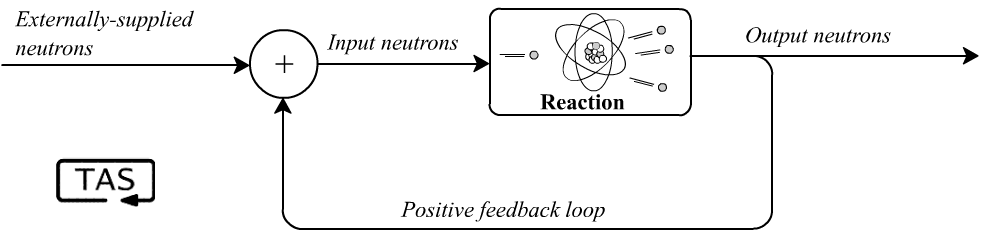
When the round-trip gain, also called the loop gain, exceeds 1, exponential growth results and the system is unstable.
While feedback is usually the culprit for instability, it’s also the cure. One of the key uses of feedback control is to allow us to harness systems that have unstable dynamics, and tame them. If your nuclear reaction is accelerating too fast, you can insert some boron control rods to absorb those neutrons and suppress the loop gain. If it slows down more than you’d like, just withdraw the rods and let it heat back up.5
When an airplane’s center of pressure is located in front of its center of gravity, it suffers from static instability, where any upwards or downwards pitch causes a torque that pitches the airplane further in the same direction. The Sopwith Camel was a famous example from World War 1, being unstable under certain loadings. It’s not impossible to fly an unstable plane, but it requires constant attention and quick reflexes. The instability gave it an advantage for maneuvering in dogfights, but it also may have killed more of its own pilots than its enemies did.

The downside of an intrinsically-unstable design is you always have to be monitoring the system and making constant corrections. Your control system can never take a coffee break.
Thus the thinking goes: In the modern era we have computers that never need coffee breaks, and never stop paying attention. So we can revisit unstable designs, and make up for the instability with fly-by-wire digital control. Can’t we?
The answer is: yes, within limits. Many aircraft today have intrinsically unstable flight characteristics, especially supersonic military aircraft, and compensate for this with computer-assisted control. But it does come with a performance penalty of its own.
Just as when we looked at right-half-plane zeros, good control is a must, but even the best control can’t fully make up for a badly-behaved system. As Gunter Stein illustrated in the classic paper Respect the Unstable, even with the best possible control system to stabilize it, a system with intrinsic instability carries an unavoidable cost paid in increased process sensitivity.6 This is due to the waterbed effect, which is driven by Bode’s sensitivity integral and is independent of the controller:

What that means in practice is that unstable hardware will always be more prone to bouncing, wobbling, oscillating, jumping, vibrating, overshooting, and crashing than a passively stable design, no matter what you do to control it.
And the price you pay is higher the more unstable your system is, and the less control bandwidth you have available.
Control bandwidth is a measure of the fastest change your control system is capable of reacting to. In other words, it describes how good your reflexes are. At one time the limiting factor to control bandwidth might have been processor speed, but these days it’s more likely to come from lag in your sensors, your actuators, or the system itself. That is, even the quickest number-crunching in the world won’t help you if:
your sensors aren’t comparably quick to report a change;
your servos aren’t comparably quick to move where you tell them;
the system has a delayed reaction, or worse, it goes the wrong way first.7
When your system is too unstable and the available control bandwidth is too low, your feedback designer gets squeezed from both sides into an untenable position, and it gets harder and harder to stabilize the system at all.
Process sensitivity is always the enemy of good control performance, but Bode’s integral defines a fundamental limit on how much you can do about it.
So what does it actually take to stabilize an unstable system? I’ll try to offer both an intuitive answer and a mathematical one.
Magnetic bearings are a very attractive idea. Why not support a rotating shaft with magnetic fields, so the bearing runs without friction and never wears out?8 Well it turns out it is a great idea, but a fast-acting feedback controller is necessary to make it work. And if you ever try to bring a strong magnet near a steel plate without letting them touch, you’ll quickly gain an intuitive understanding for everything that I’m saying today.
So here’s a challenge worth a thousand words: Can you bring a neodymium magnet within one magnet-diameter of a steel plate / table top / refrigerator, without bringing them into contact, and without bracing your grip against the steel plate itself?
(Go ahead and try it! It’s as educational as it is difficult. But be mindful of magnet safety.)9
It’s not just the amount of attractive force that makes it difficult; it’s how rapidly that force grows as the magnet approaches the steel. At a certain distance (~12 mm for me) the rate of change of magnetic attraction exceeds the reaction time of my muscles, and I lose control of the magnet’s position. If you still think it’s just the the magnitude of the attraction that’s the issue, you can settle that question by trying to pass the magnet Operation-style between two spacer-separated steel plates — such that the net attraction force balances out — and you’ll actually find it’s even more difficult to keep the magnet in the middle of the channel without it snapping to one side or the other.10
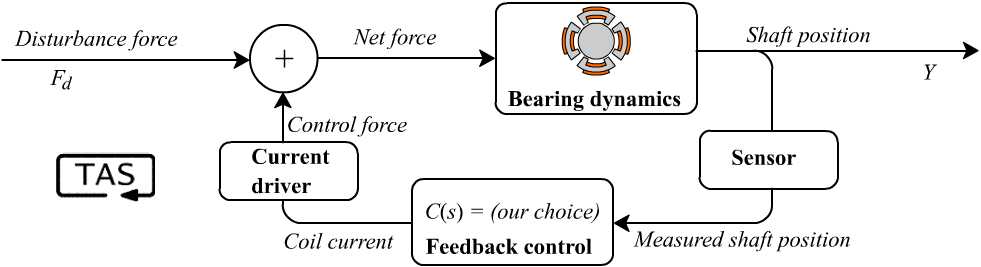
The runaway attraction between magnet and steel is an example of snap-through.11 12 13 In a magnetic bearing, the steel shaft moves and the [electro]magnet is fixed in place, but it’s the same principle at work. You definitely don’t want your shaft slamming into the electromagnet at 100,000 rpm. To fight that instability, a magnetic bearing needs a very fast-acting, high-gain feedback system, constantly measuring the shaft position and adjusting the magnetic fields in response to any deviation, to pull the shaft back to the centre before it gets snapped away. In order to stabilize it, the feedback control needs to be — at a minimum — stiffer, faster, and more aggressive than the system’s intrinsic instability.
Now let’s look at how a controls engineer might think about this instability.
(I’m going to try not to dwell too much on the fine details here so that the more broadly-applicable conclusions don’t get lost in the noise, but if you have questions about the specifics, feel free to comment!)
Stein’s paper already covers the peak sensitivity perspective, and it’s an excellent read, so instead I’ll present another approach. A very useful technique to help design a feedback controller is the root locus method, which dates back to 1948. It describes how a system’s poles move as the feedback controller is introduced. Recall that a system is unstable if it has any poles with a positive real part (= positive growth rate); the feedback controller must see to it that those poles are all moved to the left half of the complex plane where exponentials decay, rather than grow.
For an ordinary mass hanging from an ordinary spring, a force F applied to the mass results in a motion Y according to the Laplace-domain transfer function:14
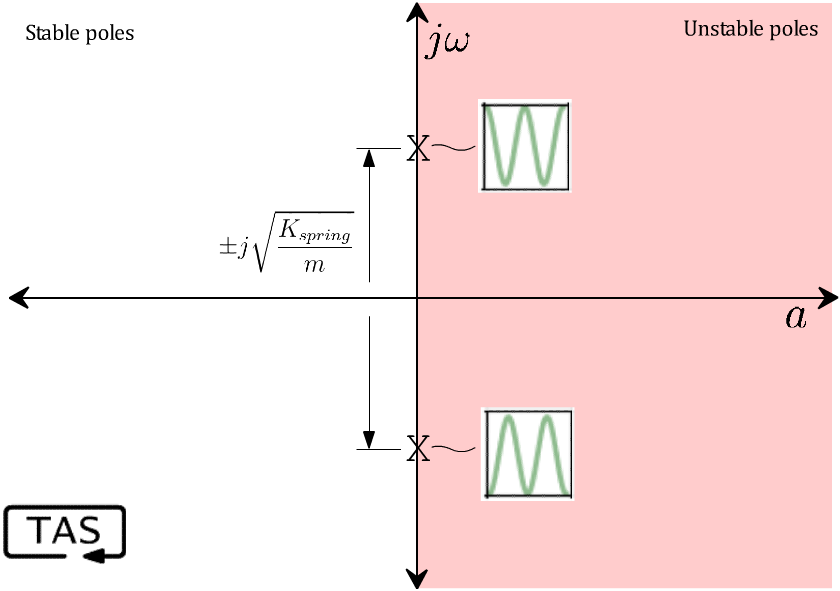
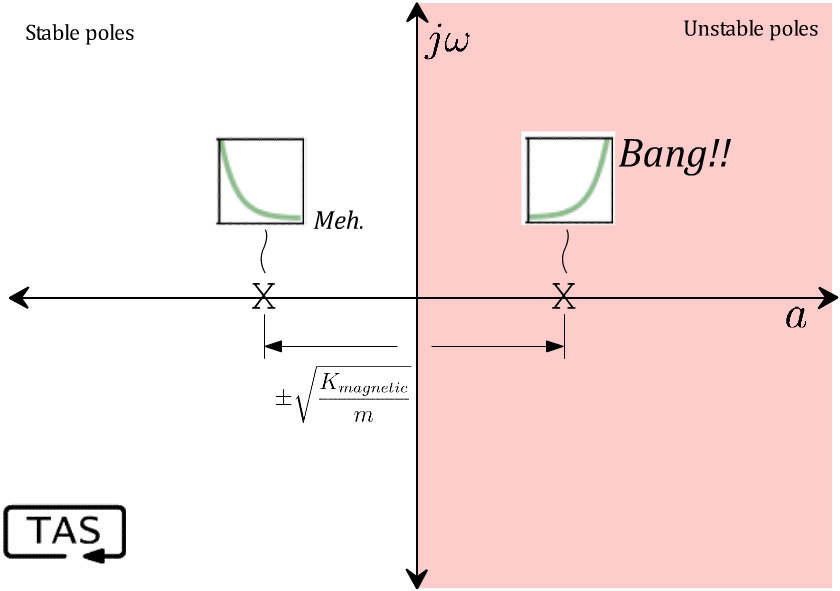
You know just by looking at it that this thing is going to oscillate up and down, and the math agrees. The poles of the system are any values of ‘s’ that create a division-by-zero. In this case, that’s a pair of resonant poles on the imaginary axis, with a frequency of √(K/m), which is here on our “zoo” of behaviours:
On the other hand, the magnetic bearing requires a permanent magnet or DC current to balance against the weight of gravity, Fₘ = mg, where m is the mass of the shaft and g is gravity. The magnetic field which creates that force also establishes a negative stiffness, dFₘ/dy, which increases inversely with the airgap between the shaft and the bearing’s inner radius:15
With the magnetic field acting as a negative-stiffness spring, the K in the bearing’s transfer function flips sign:
Where earlier we had oscillatory imaginary poles, the magnetic field’s negative stiffness instead puts those poles on the real axis, creating a response that is a combination of exponential decay and… exponential growth:
So, that’s not good.
(Interestingly, this exponential growth rate is independent of the weight of the shaft, and depends only on gravity and the width of the bearing’s airgap, so a 1 mm airgap corresponds to a 22 Hz pole, or an error that doubles every 5 milliseconds(!)):
And even undamped oscillation would have been bad enough. To make a system nicely behaved, the poles should all be generously in the left half plane, where they decay quickly enough to have a good damping ratio. Let’s add feedback control.
Let me take this chance to clarify something here. There’s nothing we can do to change the bearing’s natural, intrinsic dynamics, short of redesigning the hardware. The bearing itself will always have unstable poles. But that’s OK; once we’ve closed the feedback loop, the combined system takes on new dynamics, with its own poles, which will be different than the bearing’s old, “open-loop” poles (unless C(s) = 0). As long as these new closed-loop poles are stable, our magnetic suspension will be OK.
Assuming the sensor and driver are ideal, our closed-loop feedback system has the following transfer function:
With the feedback controller appearing in the denominator, we now can directly manipulate the poles of the closed-loop system (which again, are the values of s that make this fraction divide-by-zero). So as we ramp up the aggressiveness of our controller C(s), the closed-loop poles will start to move from ±√(K/m) to other positions in the plane. We need to get them both on the left side.
If we use just a proportional controller C(s) = Kₚ, which creates a “digital spring” to cancel out the negative magnetic spring, then the poles slide toward each other, meet at s=0 when the controller exactly cancels the magnet, and then bounce up the vertical axis as the controller gets stiffer. They never cross fully to the left, stable side. Not good enough.16
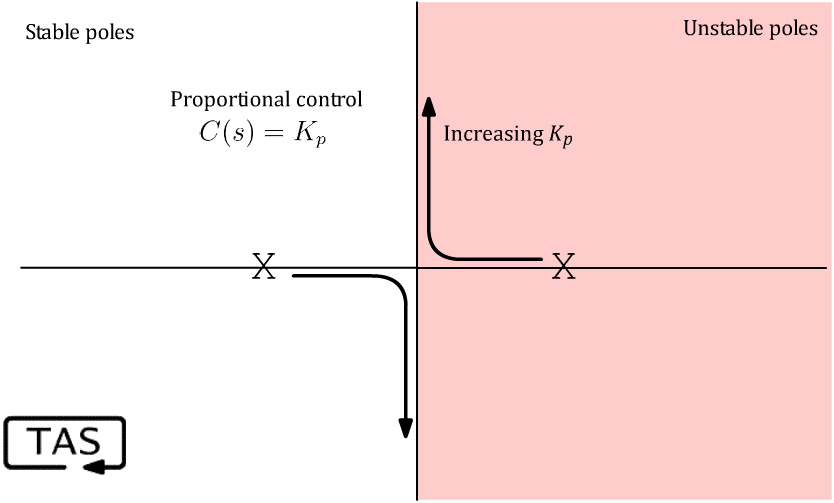
But this does provide a useful first lesson: to even achieve this borderline result, the controller needs a high enough gain to create a virtual spring Kₚ that is stiffer than the magnetic attraction causing the instability. They’re arm-wrestling and the feedback controller needs to win that contest, or we won’t have any chance at all.
We haven’t exhausted our options though; we get to design C(s) from scratch, so we have authority over its whole dynamics. Our control algorithm can do anything we want, as long as it respects causality. It can have its own poles and zeros, which we can use to coax the closed-loop poles over to the left half.
I’ll admit that root locus takes some practice to visualize.17 But one of the general principles is that, as the controller gain ramps up, the poles are attracted to the zeros.18 So by putting a zero in our controller on the left side, we can tug the poles over to the stable zone.
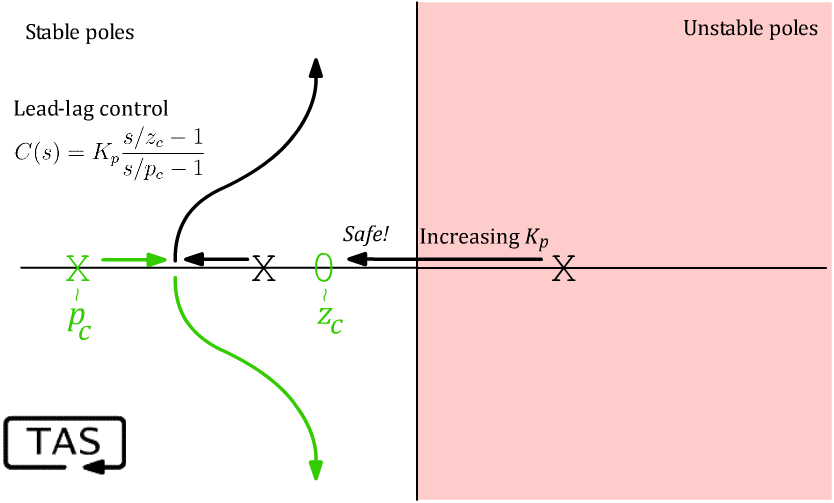
We can’t add only a zero, though. Causality requires that any realizable system must have at least as many poles as it has zeros. So we need to add a pole to our controller, too, and make sure it doesn’t cause trouble. In order to work, that controller pole has to be at a higher frequency than the zero, and to have any hope of good performance, it must be at a higher frequency than the open-loop poles.19
So that’s the second lesson: our feedback controller needs high enough bandwidth — fast enough reflexes — to be faster than the unstable system it’s controlling.
On paper, this looks easy. We can program any C(s) we want, right? It’s just lines of code in a microprocessor, after all, and it’s not like there’s a shortage of big numbers. If we need high gain and lots of bandwidth, then what’s the problem? So let it be written, so let it be done.
The problem is that every element of the feedback system needs to be fast enough to handle this. An aggressive algorithm is no good without hardware to back it up. For example, if our position sensor has some delay, that limits our bandwidth. If our current regulator tends to move the wrong way first, that limits our bandwidth too. These are hard limitations; they cannot be programmed around, and they cannot be fully corrected by any kind of intelligent look-ahead prediction.
Time delays in a feedback loop are lethal to control stability. A time delay of τ throws a half-circle of radius ~1/τ Hz onto the root locus that pushes the poles away to the unstable side. We’ll find ourselves needing to pull more tricks with our controller to maintain stability, and making more compromises in the process.
As the delay is increased, that circle tightens, overwhelming anything that the controller might do to stabilize the system. If the delay exceeds √(m/K), the system becomes not only unstable, but unstabilizable.
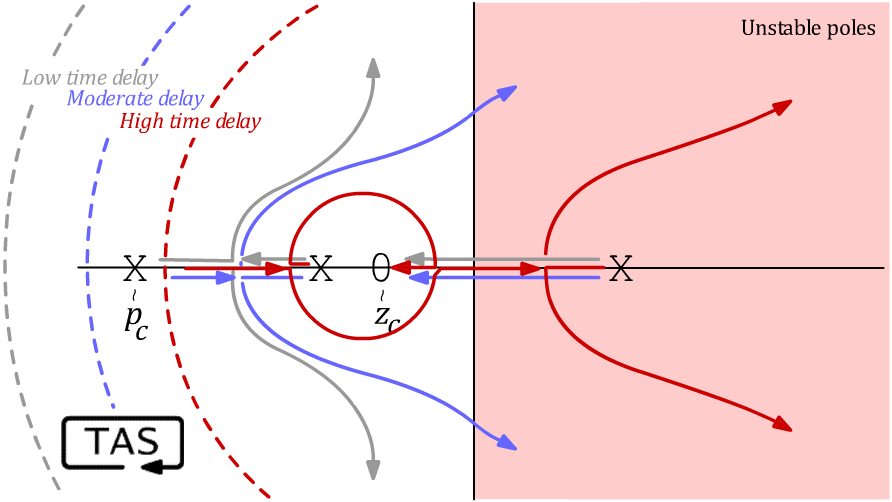
Here’s what I mean by “making compromises”:
But right-half-plane zeros are even worse. (AKA inverse response, or moving the wrong way first). Remember, poles are attracted to zeros! If something introduces a zero to the right-half-plane, that’s going to greatly complicate our efforts to get any unstable poles out of there. Or worse, it could drag otherwise stable poles toward it like a black hole. And the slower that inverse response acts, the closer to the origin the zero is, and harder it gets to deal with. Once that zero gets between the unstable pole and the origin, we lose all hope of stabilizing the system.
And I haven’t even gotten to other non-idealities like output saturation, slew rate limits, and hysteresis. All of them can create conditions that make an unstable system unstabilizable.
So that’s the third lesson: every hardware component in the loop needs to react at least as fast as the system’s unstable poles. If your sensor doesn’t cut it, then no amount of control optimization will make up for that.20
And, even after you’ve done all this work to stabilize the system, those poles will still end up closer to the right-half-plane than they would have if some hadn’t started there to begin with. That means less damping and slower decay, so the closed-loop performance just won’t be as snappy or reliable as it would have been if it were built on an intrinsically stable system to begin with.
But let’s not miss the forest for a detailed inspection of one tree.
None of this is specific to magnetic bearings. The same core mathematics apply to supersonic aircraft, nuclear power stations, rocket guidance, bipedal locomotion, bacterial growth, epidemics, and any other system capable of sustaining exponential or super-exponential growth. I think Stein makes this point better than I can when he urges us to maintain a great deal of cautionary respect for all unstable systems, no matter their nature, universally united by the Bode integral.
What I’m hoping you’ll take away is not factoids about magnets, but just a basic and widely-applicable lesson about instability: Whenever you spot a positive feedback loop at play, take heed. For every unstable pole in the system, faster and more aggressive control effort is required, and the system becomes more dangerous and less controllable.
Engineering such systems requires humility, and a mindset that acknowledges intrinsic control limitations at the outset rather than sweeping them under the rug and assuming that software, experts, or undeveloped technology will deal with any problems down the road.
“Not so fast!”, I hear from the back of the audience.
“In the modern world our systems are complex, nonlinear, multi-input, interconnected, time-varying, chaotic, have no good models, have unknown internal relationships, and so on! Surely none of this 1940s linear systems theory stuff is relevant! Why should I heed these ominous lessons?”
There are many answers I could give, but for now I’ll say: an engineer’s paramount responsibility is ensuring the safety of their work. Heaping additional uncertainty into an already unstable recipe is, frankly, not a reason to increase one’s confidence in future good outcomes. We shouldn’t let epistemic uncertainty stop us from thinking, but adding unknowns to the mix always broadens the distribution, and requires correspondingly higher care and precaution if we want to avert the worst outcomes.
Because frequently, the failure of unstable systems comes with a price paid in dollars, jobs, environmental destruction, and sometimes human lives.
This post isn’t intended as professional engineering advice. If you are looking for professional engineering advice, please contact me with your requirements.
Linear systems produce exponential behaviour because y = eᵏᵗ is the solution to the (linear) differential equation dy/dt = ky. Even though there are many diverse linear systems with various governing equations, they always have exponential-like responses because the exponential growth function (eᵏᵗ) is the eigenfunction of the time-derivative operator d/dt, meaning that exponentials are the native language of linear differential equations. (Sine- or cosine-like oscillation counts as “exponential-like” because cos(ωt) = ½(eʲʷᵗ + e⁻ʲʷᵗ), by Euler’s formula).
A system’s homogeneous response may be composed of several exponentials added together, and the coefficients k might be positive (exponential growth), negative (exponential decay), imaginary (oscillation), or complex (some combination of growth/decay/oscillation). If any of those exponential coefficients have a positive real part, the system’s growth rate is positive, and it is therefore unstable.
Most systems that grow exponentially do eventually reach some carrying capacity, at which point the exponential growth slows, stops, or reverses. This means that those systems aren’t perfectly linear, but may be very nearly linear below some limiting threshold. Because the system behaves linearly up to that point, that threshold usually cannot be estimated by examining the growth trend itself.
Although, the knowledge that any runaway growth must eventually end isn’t always comforting, because that ending usually takes the form of a circuit board catching fire.
"Nonlinear” is a vague term and can refer to both faster-than-exponential and slower-than-exponential systems (ie diminishing returns). A bacterial growth system is nonlinear, because as the population increases, the available resources for further growth diminish, which results in growth that is initially exponential but slows down over time. Nonlinear systems that undergo superexponential growth usually can’t keep it up forever either, and eventually transition into a subexponential growth or contraction phase once they’ve exhausted their capacity.
This isn’t a post about nuclear engineering, and of course there’s a lot more to it. An important consideration is how likely it is that each output neutron goes on to produce new fission reactions. In most reactor designs, neutron moderators are used to increase that probability, and adjusting the moderator behaviour is an effective way of keeping the reaction self-stabilizing.
The actual operation of control rods in a nuclear reactor is a bit more complicated than a standard linear feedback controller, because rather than just directly subtracting neutrons, the control rod position modulates the (average) gain of the reaction feedback loop itself, so they can shift the reaction from being intrinsically stable to intrinsically unstable.
I don’t want to create the wrong impression of nuclear safety here. Modern nuclear reactor designs are tremendously safe and I believe that they are an essential part of a clean, low-emissions power grid.
But I also don’t want to create confusion between safety and stability in an essay that is primarily concerned with the latter. For the sake of precision, modern nuclear reactor designs are passively safe, if not always passively stable. Even if the control system fails or loses power, the reactor is designed to shut down automatically via failsafe mechanisms. For example, the control rods may be suspended by electromagnets, dropping into the reactor automatically if backup power is lost, shutting it down fast. Older reactor designs relied more on active systems to shut down, which weren’t always present in an emergency. New designs also tend to avoid relying on water as a failsafe coolant, because thermolysis can occur when water comes in contact with superheated surfaces, resulting in an explosive buildup of hydrogen, as occurred at Fukushima.
Nuclear reactors may also be passively stable in most operating regimes. For example, as the nuclear fuel heats up, thermal expansion reduces the probability of neutron absorption, reducing reactivity and passively stabilizing the reaction as a built-in negative feedback that reaches a stable equilibrium on its own, requiring control rods only to adjust that equilibrium to the power output requirements.
Chernobyl was itself designed to be passively stable in its normal operating mode, but not passively safe. At low output power it lacked passive stability, but with a growth rate that was slow enough for the control system to keep up as it transitioned into a higher-power regime. However in the particularly extreme case that triggered the accident, the unstable pole was pushed to such a high frequency that the growth rate overwhelmed any control response as well as the passive feedback mechanisms, and the presence of graphite tips on the boron control rods effectively added a right-half-plane zero that limited the control bandwidth and made safe recovery impossible.
This may be a controversial statement to make, but I would argue that even the Chernobyl RBMK reactor design was engineered to a very safe standard, with redundant automatic safety systems which, even despite their flaws, should have been capable of preventing meltdown if they had not been deliberately overridden. I think one important safety lesson learned from Chernobyl is that a design must be robustly capable of preventing meltdown even in the worst case, where the control room is trying to cause one on purpose. The consequences of nuclear disaster are so significant, and their operating lifetimes so long, that they need to be robust against extremely unusual events.
(But also, don’t put graphite tips on your control rods, please).
Process sensitivity (traditionally given the symbol S) describes how much the presence of a feedback controller amplifies a system’s reaction to disturbances to its measured output. (Such disturbances always exist, and can occur due to sensor noise, or due to the system’s actual dynamics being slightly different from what a model would predict).
A feedback control system by-and-large makes the system behave better (and if that system is open-loop unstable, then without feedback it would be completely unusable). But everything has a price, and no lunch is free. Feedback will improve a system’s performance in the part of the spectrum we care about the most, usually frequencies near DC. But as Bode’s sensitivity integral shows, it will always come with an accompanying reduction in performance distributed across the rest of the spectrum.
It’s also bad if your system has a varying or unknown reaction at high frequencies, although in this case there’s always the glimmer of hope that sufficiently-advanced system identification techniques can discover them and adapt the controller accordingly.
Air bearings are an easier way to do this, so magnetic bearings tend to be used when air bearings can’t: in vacuum, or for ultra-high-speed rotation where the shaft surface speed approaches some multiple the speed of sound. The niche demand for such applications, moreso than the technical difficulty of magnetic suspension, is probably why active magnetic bearings are still not cheap commodities. Although they are showing up a lot in oil-free chiller compressors these days, where their main advantage is reduced power consumption and associated heating.
There are some passive magnetic bearings that operate on other principles. Diamagnetic bearings, superconducting levitation, and eddy-current levitation are all passive methods for magnetic suspension, although they have their own downsides.
Always be mindful of magnet safety. This experiment is best done with a neodymium magnet smaller than about 0.5 cm³. Anything bigger and you risk a painful pinch. (Yes, I know my magnet is twice that size). Even small magnets can be dangerous if they fly together and shatter. I recommend putting a cloth or mousepad over the steel plate both to reduce that shatter risk and also to make it easier to retrieve the magnet after inevitable failed attempts. Simple tools, such as pliers or vise-grips, are allowed as long as they also don’t touch the steel plate. But be mindful of the magnet grabbing them too. The magnet should be oriented so that its pole is facing the steel plate. Wear safety glasses.
This is an even more fun experiment, but most people don’t keep rigid steel plates or U-shaped steel channels at home.
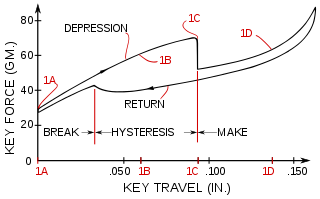
“Snap-through” is a term for the unstable motion of any mechanical system with a negative stiffness characteristic. Negative stiffness is a rather counterintuitive phenomenon, because we tend to have much more experience with systems that have positive stiffness: a restoring force proportional to displacement. When you push on an ordinary positive-stiffness system (such as a chair), it pushes back. When you push on a negative-stiffness system, it flies away suddenly, until something else eventually catches it. Such systems rely on releasing stored energy. The most familiar example is a keyboard key; after a certain point in the depression, the spring buckles and the key snaps down under the weight of your finger.
Try pressing your spacebar halfway down and holding it there.
(Go ahead, try it! There are no safety issues this time.)
The only way you can achieve this is by controlling your hand in “displacement mode”, where you stiffen your muscles and try to move a fraction of a millimetre at a time. As long as the passive stiffness of your hand is greater than the negative stiffness of the spring, you can manage it. In “force mode”, you won’t have a chance.
Magnetic attraction is both unstable and nonlinear, because the closing force goes with 1/(airgap²). A digital control system can transform it to a linearized system, but the controller aggressiveness still has to increase as the airgap closes to keep up with the moving poles. Small airgaps can require a dramatically higher sampling rate just to keep up with the required control bandwidth. Still, a well-performing feedback controller will maintain a nearly-constant airgap, which makes the system’s nonlinearity fairly negligible. But even when the nonlinearity can be neglected, the instability always matters.
The parameter ‘s’ is the Laplace transform parameter, and can be thought of either as a frequency or as an exponential growth rate. I’ll have another post on the Laplace transform that explains where s comes from, as well as how the Laplace transform works, why it’s useful, and (hopefully) makes it intuitive, but for now you’ll have to bear with me.
“Pole” is also the correct technical term for the north- or south-polarized face of an electromagnet, but I’m avoiding that usage of the word for hopefully obvious reasons. This unfortunate namespace collision is really annoying across the field of motor control, and I suspect that the confusion is sometimes exploited deliberately by marketing departments.
You might wonder why just reaching the imaginary axis is not good enough. After all, the instability is gone, right? Here are some reasons why:
Even if we could achieve such a result, undamped oscillation will destroy the bearing. With no damping, the energy of accumulated disturbances would build up over time to increase the vibration amplitude until the motion was more than the gap width, creating contact between the shaft and bearing.
The attraction between shaft and bearing increases with the position error, so the required control gain would actually vary if the shaft were allowed to move substantially off-centre. If our controller were capable of keeping those errors small, we wouldn’t have to worry very much about that nonlinearity, but as noted above, proportional control fails to do that.
We can’t actually implement perfect proportional feedback control. Even with a fully-analog control system, there will be response-time delays in the position sensor and the coil current regulator, limiting our system bandwidth and making our proportional control only good up to a finite frequency.
Also, if you’re thinking we should tune the proportional controller such that the poles just touch the origin without resonating… sorry, that’s not good either. The resulting suspension is a free body with no stiffness at all, so instead of bouncing, the shaft will just drift away from centre until it makes hard contact.
I can’t go in-depth on the root locus technique in this article without excessive scope creep, but I hope to cover it in a future article. I’ll just mention one thing:
Technically the root locus can be calculated for a sweep of any system parameter, but it’s almost always controller gain. You might think that means it’s only useful for designing proportional controllers, but that’s definitely not the case. I prefer to think of it as putting a soft on-switch on the controller, ramping it from 0 to 1, and showing how the controller modifies the system as it is gradually brought into action. So if I am considering a controller design C(s), I’ll sweep the root locus of G•C(s) for parameter G ranging from 0→1.
The closed-loop poles don’t always move toward the open-loop zeros in a straight line, but as the feedback gain increases, that is their destination.
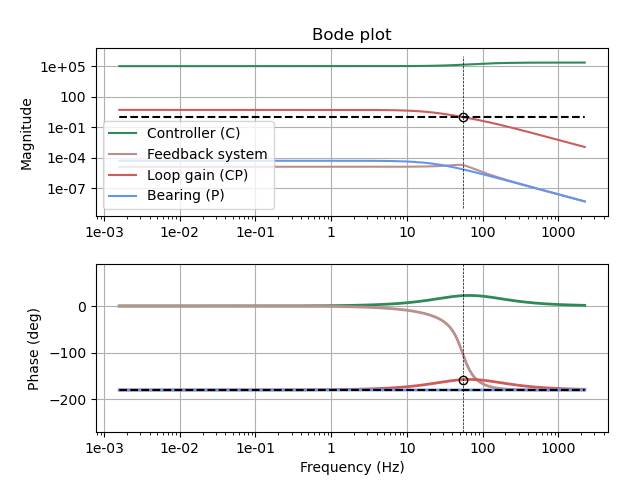
You can see this just from looking at the Bode plot. How? I’ll try to give as brief an explanation as I can…
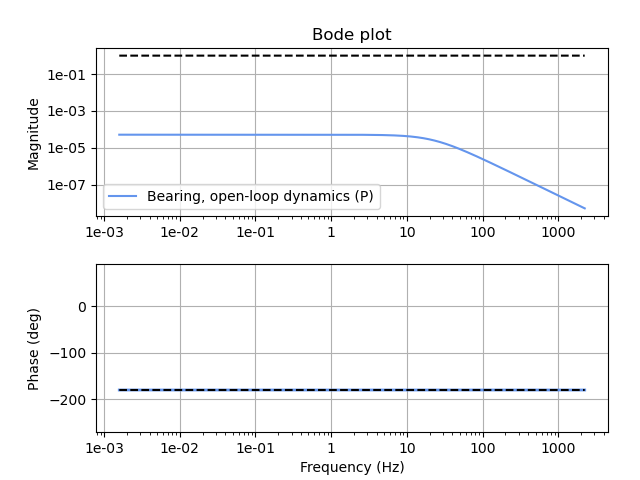
Due to the position of its poles, the magnetic-bearing system has, interestingly, 180° phase at all frequencies. We need to add some phase margin to stabilize the system, and adding a zero is how we buy that. (Phase margin is how far the phase is above 180° at the crossover frequency: the frequency where the loop gain drops below 1). But a system must have at least as many poles as it has zeros in order to be causal; an acausal system is not physically realizable. So the zero we add has to at least come as a zero-pole pair. To get useful phase margin we need the crossover frequency to be somewhere above the controller zero and below the controller pole.
The crossover has to occur where the loop return ratio magnitude has a downward slope. But controller transfer function has an upward slope over the frequency band from its zero to its pole. So to get a cleanly defined crossover, the crossover has to occur where the plant contributes to a descending magnitude, which is above √(K/m) (at ~22 Hz in the plot below).
Therefore, the controller pole should be at a frequency higher than 22 Hz, and perhaps more importantly, the crossover frequency must too. The controller must have sufficient bandwidth for this, so the feedback system must be faster than the plant’s instability.
There are some approaches to help deal with deadtime, such as the Smith predictor, which estimates the effect of a corrective control effort on a predictive model of the system. However these approaches still cannot avoid a delayed response to unmeasured disturbances, are very sensitive to small modelling errors, and struggle with intrinsically-unstable systems where the exponential growth rate is comparable to the delay time.
Failing that, there are some control approaches that can attempt to bound the error without fully stabilizing the system, like switching control, which is actually illustrated in the Sopwith Camel sketch. The article is already too long to go into detail here but there’s still no free lunch; the error bound you can enforce on the system will depend on the total unmeasured noise, the unstable growth rate of the system, and how rapidly you can switch. And even after pulling out all stops, actuator saturation, slew rate limits, or system nonlinearities can still prevent the error from even being held within a finite band.
Your last hope for true stability would be to take the bearing design back to the drawing board and increase the airgap, slowing down the system’s intrinsic instability. That may or may not be an option.








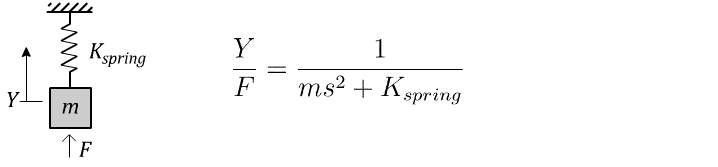
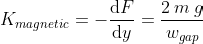
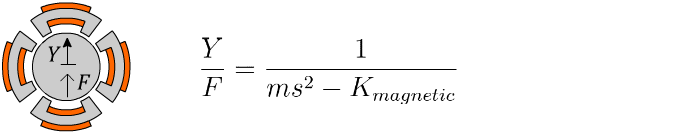
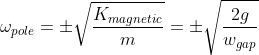
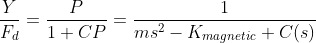

> The actual operation of control rods in a nuclear reactor is a bit more complicated than a standard linear feedback controller, because rather than just directly subtracting neutrons, the control rod position modulates the (average) gain of the reaction feedback loop itself, so they can shift the reaction from being intrinsically stable to intrinsically unstable.
Nuclear reactors are also frighteningly complicated control systems because of delayed neutrons. The classic image of a bomb-like chain reaction is one of "prompt criticality," where nuclear fission produces new neutrons near-instantly that (can) cause more fission reactions, and so on. The timescales of this reaction are so quick that physical control would be impossible — nuclear core detonations are faster than the speed of sound in the core, after all.
However, nuclear reactors are saved through delayed neutrons; a small fraction of neutrons flying around the core come not from the fission itself, but from the decay of short-lived fission products. This timescale is still relatively fast (a few fractions of a second), but it's slow enough for control systems (passive or active) to maintain the reactor in a stable state. The reactor is "prompt subcritical" with respect to the direct fission neutrons, but held at criticality after the contribution of delayed neutrons.
You explained what the distance along the real axis implies, but what about the distance along the imaginary axis?